Time-scale invariant processe
The investigation of random processes characterized by a wide range of scales
is becoming increasingly important in many experimental fields ranging fom the
investigation of earthquakes in earth-science, to turbulence in fluids, to the
behavior of returns in financial markets. In particular, many random processes
exhibit a time-scale invariant structure. Someone describes this asying that
"the scale invariance is originated from the fractal nature of the signal"; though
meaningless, such a sentence is quite evocative. The self-similarity of the signal is
reflected in the power law behavior of the power spectrum
S(f) = 1/fα, , which lacks
characteristic time scales. Notable examples of self invariant signals also
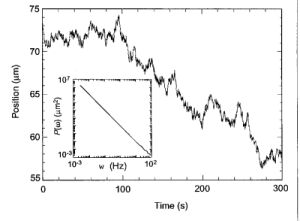
include the heartbeat, the position of a brownian particle and many others.
A bibliographic data base about time-scale invariant processes is one-over-f noise.